simple harmonic oscillator
The concept of oscillation is fundamental in acoustics, such as in the motion of a guitar string or the vibrations of a cymbal. Among various types of oscillators, the simple harmonic oscillator (SHO) stands out as a foundational model. Simple harmonic motion (SHM) occurs when an object moves back and forth around an equilibrium position in a sinusoidal pattern. This post will consider simple harmonic oscillators, exploring their mathematical representation and characteristics.
Simple harmonic motion is governed by a few essential characteristics. Perhaps the most familiar real-life example of SHM is the mass-spring system. When the mass is moved from its equilibrium position, it oscillates, or vibrates back and forth. The restoring force provided by the spring is essential to creating this simple harmonic motion. From Hooke’s law, the restoring force is
\begin{equation} F = -kx \end{equation}
where \(x\) is the displacement and \(k\) is the spring constant. When combined with Newton’s second law of motion \(F = ma\), the acceleration of the mass becomes
\begin{equation} \frac{d^2}{dt^2}x(t) = -\frac{k}{m}x(t) \end{equation}
where \(m\) is the mass. Choosing \(\omega_0^2 = \frac{k}{m}\) and consolidating terms gives
\begin{equation} \frac{d^2}{dt^2}x(t) + \omega_0^2x(t) = 0 \end{equation}
This ordinary differential equation (ODE) is the governing equation for simple harmonic oscillators. It is important to note that this ODE is homogenous so that it represents “free” vibrations. Free vibrations means that once the mass is set into motion, no other force acts on it. As a result, its motion is entirely determined by an initial displacement and velocity. The general solution is given as
\begin{equation} x(t) = C_1 \cos(\omega_0 t) + C_2\sin(\omega_0 t) \end{equation}
where the constants \(C_1\) and \(C_2\) depend on the initial conditions. Importantly, the sinusoidal motion oscillates at the natural angular frequency \(\omega_0\). The time taken for one complete oscillation is called the period \(T\), while the number of oscillations per unit of time is referred to as the natural frequency \(f_0 = 1/T = \omega_0/(2\pi)\).
For a second order ODE, both the initial displacement \(x(0) = x_0\) and the initial velocity \(v(0) = v_0\) determine the constants. At time \(t = 0\), the displacement is
\begin{equation} x(0) = C_1 \cos(0) + C_2\sin(0) = C_1 \end{equation}
so \(C_1 = x_0\). The velocity is
\begin{equation} v(0) = \frac{d}{dt}x(0) = -C_1\omega_0\sin(0) + C_2\omega_0\cos(0) = C_2\omega_0 \end{equation}
so \(C_2 = v_0 /\omega_0\). The solution to a simple harmonic oscillator is
\begin{equation} x(t) = x_0\cos(\omega_0 t) + \frac{v_0}{\omega_0}\sin(\omega_0 t). \end{equation}
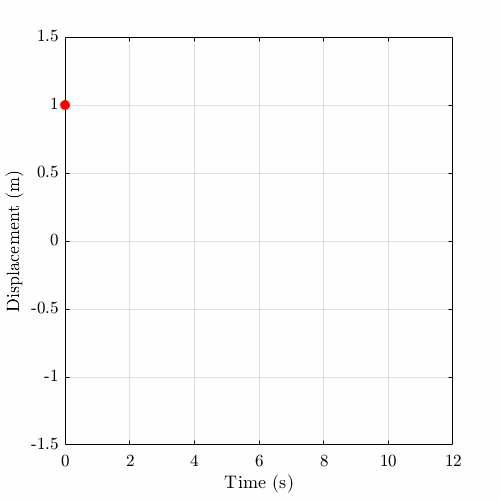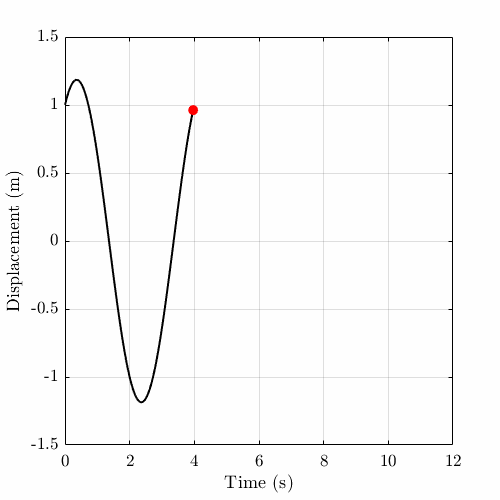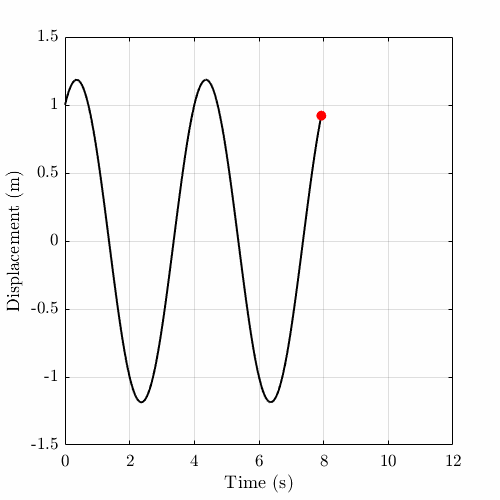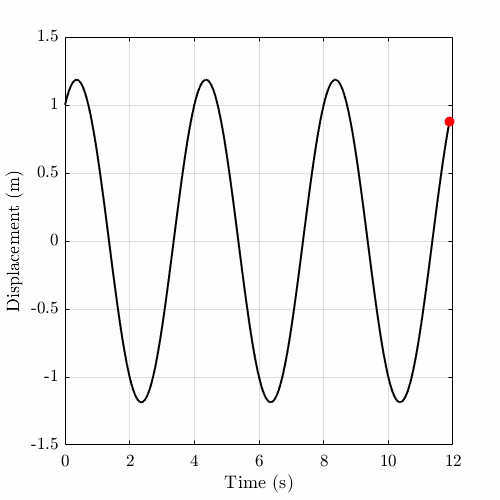
The following animation shows simple harmonic motion for \(\omega_0 = \pi/2\), \(T = 4\) s, \(x_0 = 1\) m and \(v_0 = 1\) m/s.