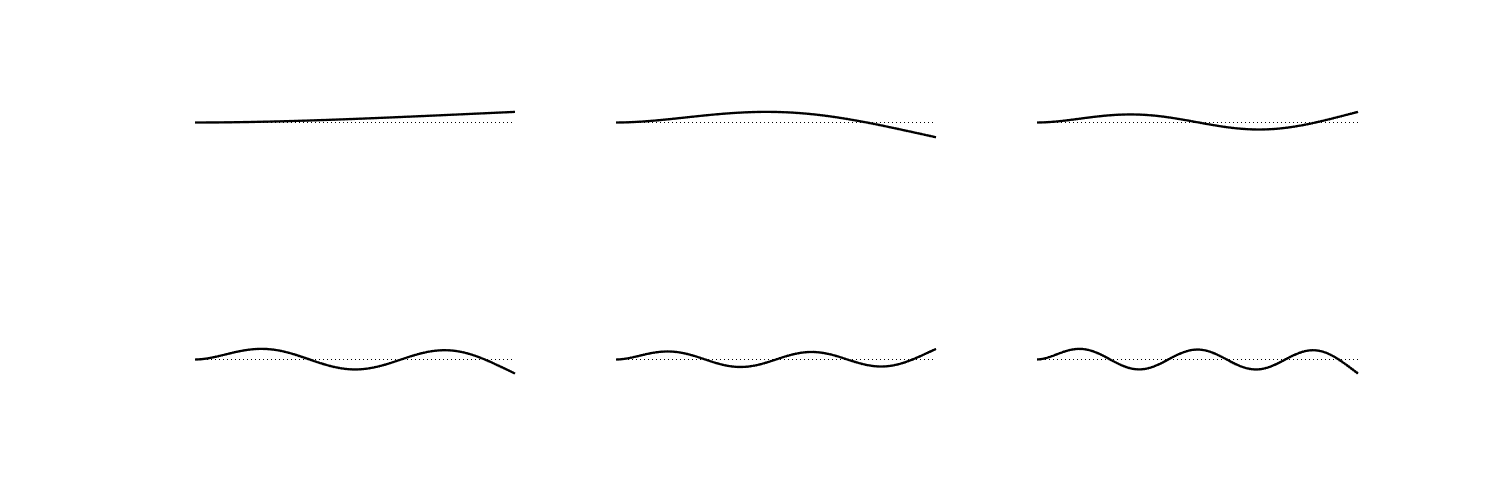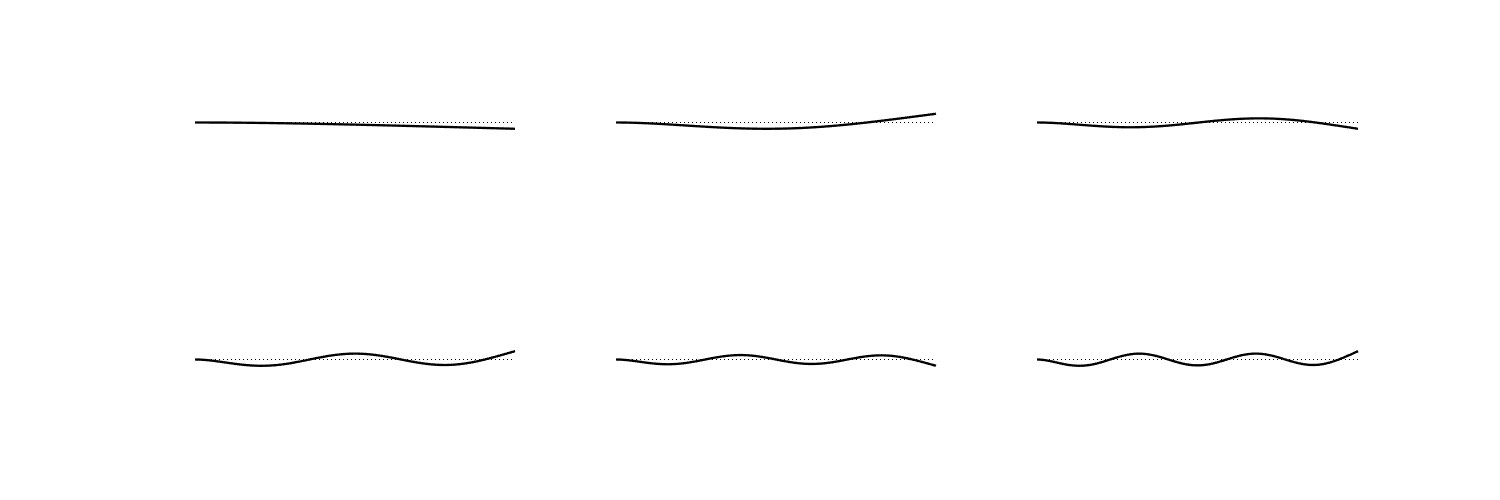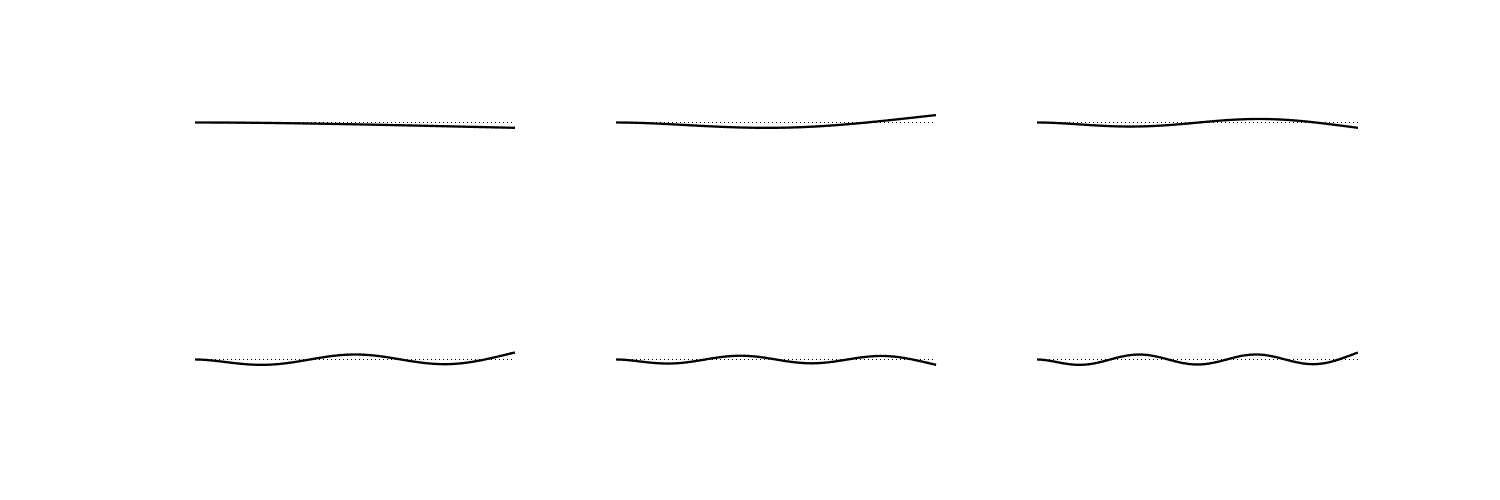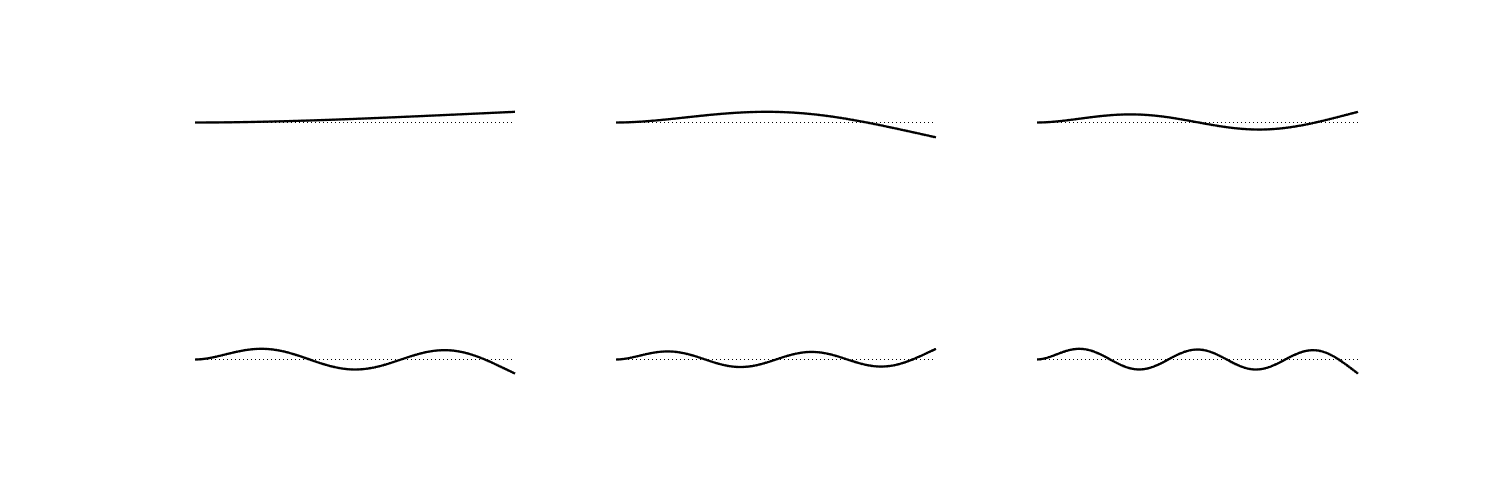
rod bending modes
A “rod” is an elastic solid whose cross-sectional area is very small relative to its length. A vibrational model constrained to one dimension serves as a good approximation to its motion.
For transverse vibrations, under the Euler-Bernoulli assumptions, the governing equation of motion for an isotropic material is
\[\frac{\partial^2}{\partial x^2}\left(EI(x)\frac{\partial^2}{\partial x^2}\xi(x,t)\right) + \rho(x) S(x) \frac{\partial^2 }{\partial t^2}\xi(x,t) = 0\]For uniform density and cross-sectional area, it simplifies to
\[EI\frac{\partial^4}{\partial x^4}\xi(x,t) + \rho S\frac{\partial^2 }{\partial t^2}\xi(x,t) = 0\]The general solution is
\[\xi(x) = A\sin k_n x + B\cos k_n x + C \sinh k_n x + D\cosh k_n x\]Different boundary conditions give different eigenfunctions and eigenvalues.
A “simply supported” rod has the following boundary conditions: \(\xi(x_b) = 0\) and \(\frac{\partial^2}{\partial x^2} \xi(x_b) = 0\).

A “clamped” rod has the following boundary conditions: \(\xi(x_b) = 0\) and \(\frac{\partial}{\partial x} \xi(x_b) = 0\).

A “free” rod has the following boundary conditions: \(\frac{\partial^2}{\partial x^2} \xi(x_b) = 0\) and \(\frac{\partial^3}{\partial x^3}\xi(x_b) = 0\).
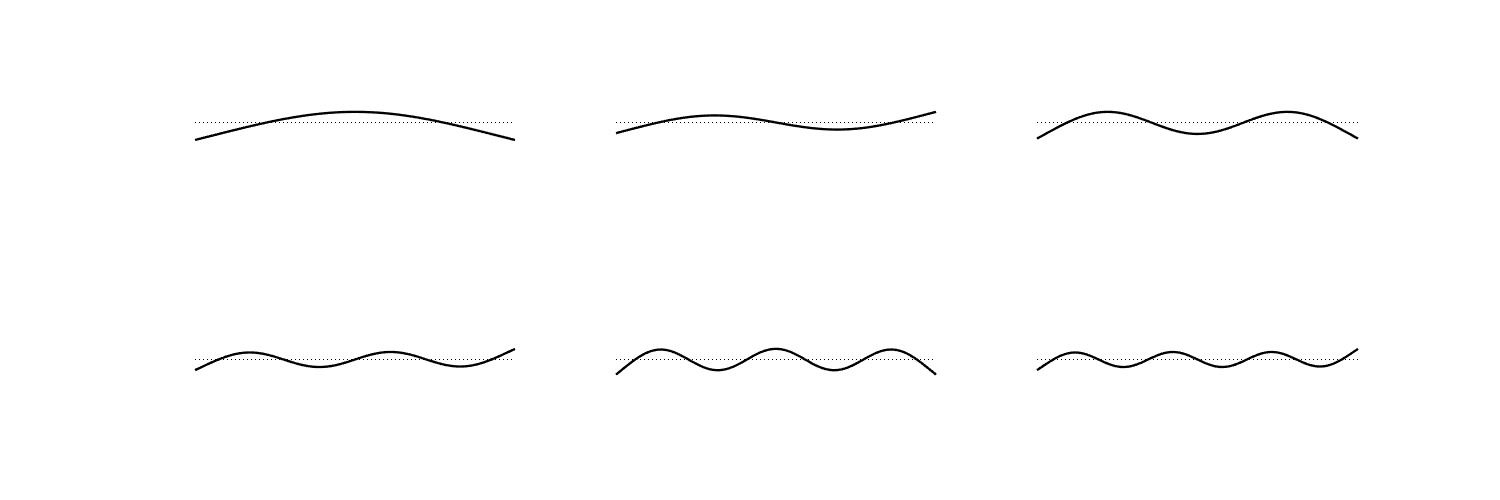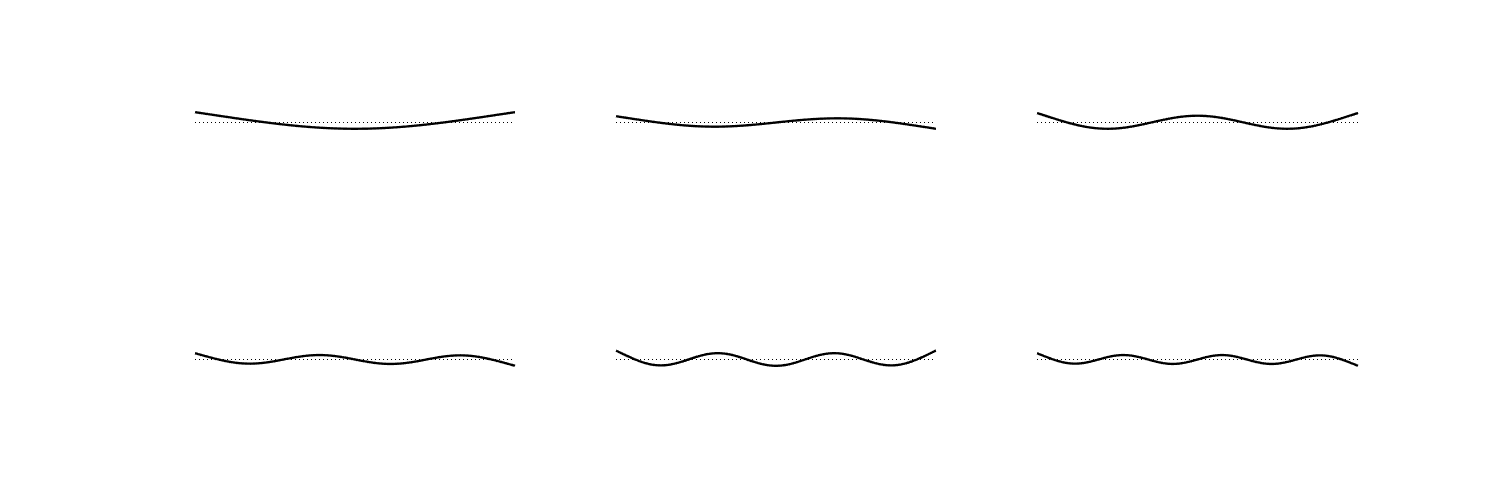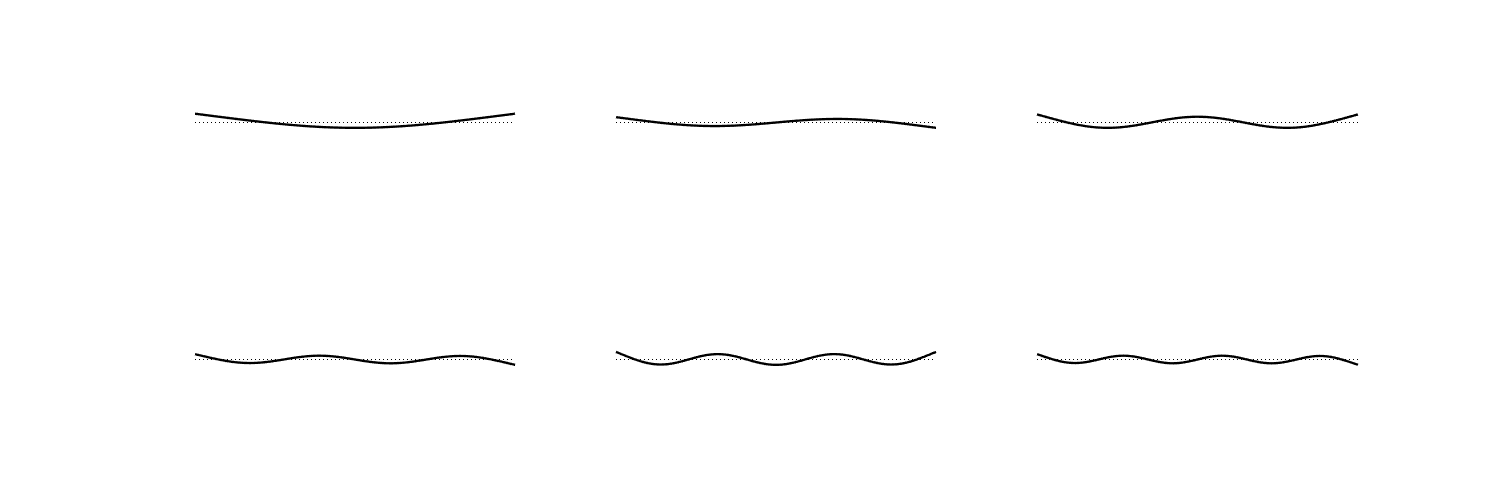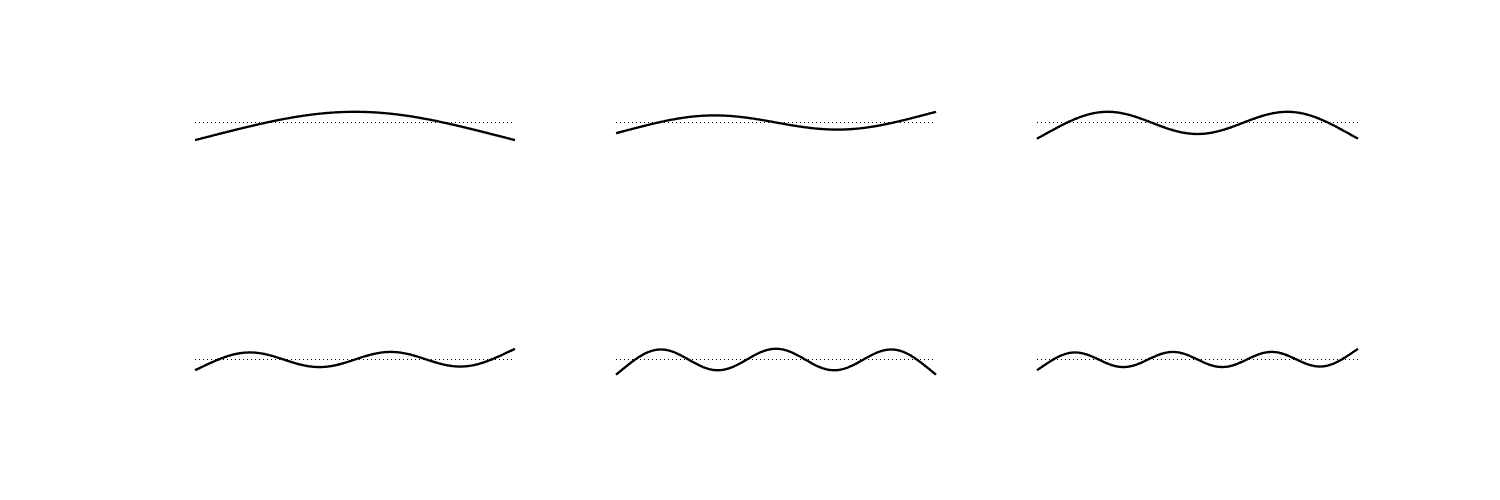
A “cantilever” rod has clamped boundary conditions on one side and free boundary conditions on the other.