scattering from a plane wave
Scattering refers to a physical phenomena when waves interact with an object. Typically, the incoming waves, or incident field, reflect or bend around this object.
To determine the pressure field in such a scenario, the typical approach is to break the total pressure into an incident field and a scattered field: \begin{equation} p_t = p_i + p_s \end{equation} The incident field is the pressure field without the presence of a rigid scatterer. The scattered field is solved for by satisfying boundary conditions.
For a plane wave scattering on a rigid sphere, the incident field is a plane-wave: \begin{equation} p_i(r,\theta,\phi, k) = e^{-i \mathbf{k} \cdot \mathbf{r}} \end{equation} However, it is convient to express this in terms of a spherical harmonic expansion later when we need to match boundary conditions. \begin{equation} p_i(r,\theta,\phi, k) = 4\pi \sum_{n=0}^\infty\sum_{m=-n}^n(-i)^n j_n(kr)Y_n^m(\theta,\phi){Y_n^{m}}^*(\theta_i,\phi_i) \end{equation}
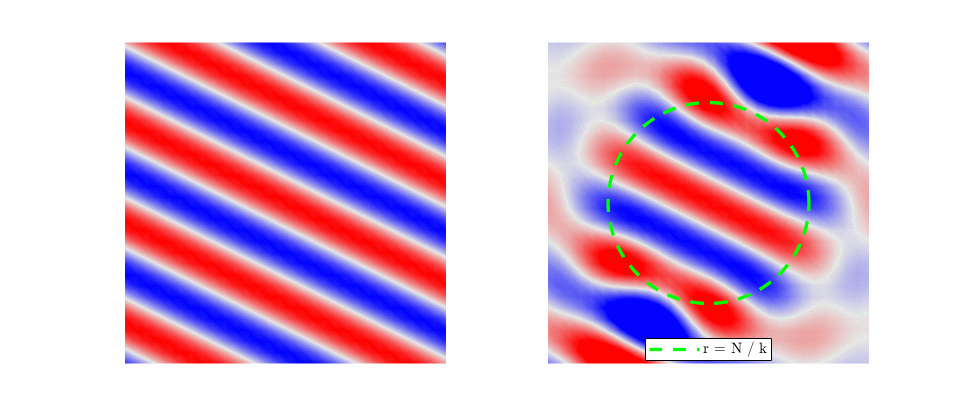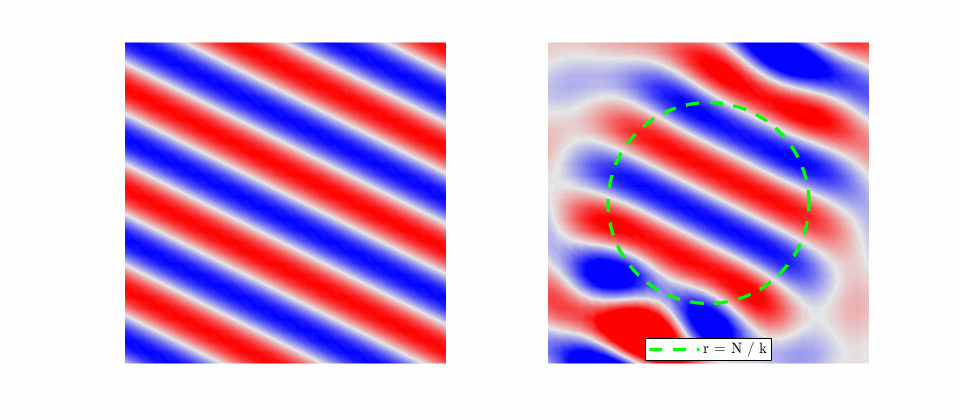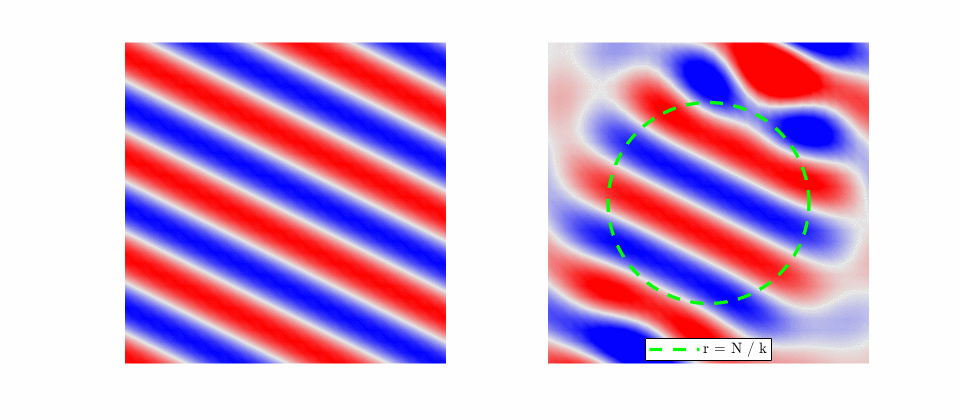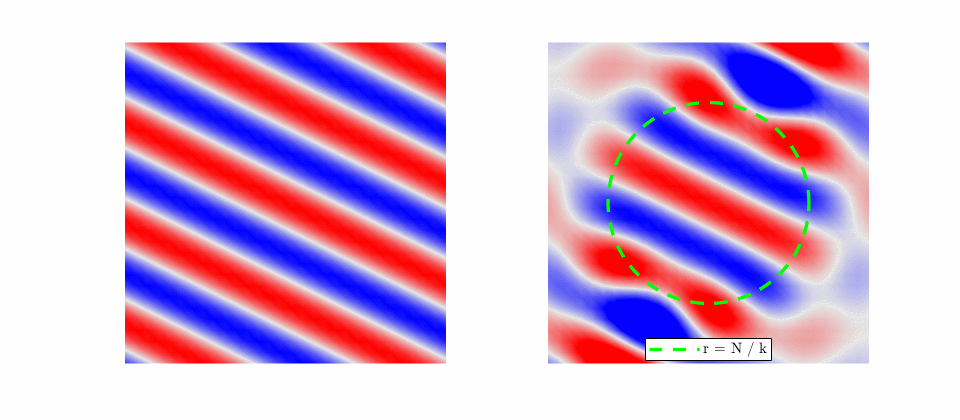
Next, choose for the scattered field outward propagating waves that decay to zero at infinity. The scattered field will have the form \begin{equation} p_s(r,\theta,\phi,k) = \sum_{n=0}^\infty\sum_{m=-n}^n c_n^m(k)h_n^{(2)}(kr)Y_n^m(\theta,\phi) \end{equation} where \(c_n^m\) are the unknown expansion coefficients that must be solved for.
For a rigid sphere, the normal derivative of the total pressure must be zero. This implies \begin{equation} \frac{\partial}{\partial r}p_t = \frac{\partial}{\partial r}p_i + \frac{\partial}{\partial r}p_s = 0 \end{equation} which implies \begin{equation} \frac{\partial}{\partial r}p_s = -\frac{\partial}{\partial r}p_i \end{equation} This equation tells us that if we know the normal deriavite of the incident pressure, we can determine the scattered pressure. Differentiating both the incident and scattered field wrt to r and evaluating at the surface of the sphere \(r = a\) gives
\begin{equation} \sum_{n=0}^\infty\sum_{m=-n}^n c_n^m(k)h_n^{(2)’}(ka)Y_n^m(\theta,\phi) = - 4\pi \sum_{n=0}^\infty\sum_{m=-n}^n(-i)^n j_n’(ka)Y_n^m(\theta,\phi){Y_n^{m}}^*(\theta_i,\phi_i) \end{equation}
Applying Fourier’s trick and mutliplying each side by an arbitrary spherical harmonic and integrating results in
\begin{equation} c_n^m(k)h_n^{(2)’}(ka) = - 4\pi (-i)^n j_n’(ka){Y_n^{m}}^*(\theta_i,\phi_i) \end{equation}
The scattered expansion coefficients become \begin{equation} c_n^m(k) = - 4\pi (-i)^n \frac{j_n’(ka)}{h_n^{(2)’}(ka)}{Y_n^{m}}^*(\theta_i,\phi_i). \end{equation}
