spherical harmonics
Spherical harmonics \(Y_n^m(\theta,\phi)\) are special functions defined on the sphere. One of their most important properties is that they are the eigenfunctions of the Laplace operator on the sphere:
\begin{equation} \nabla^2 Y_n^m(\theta,\phi) = -n(n + 1)Y_n^m(\theta,\phi). \end{equation}
As a result, they appear in numerous applications including solutions to Laplace’s, the wave, and the Helmholtz equation. They are used extensively in spatial audio applications such as ambisonics, source directivity representation, and spherical array signal processing techniques.
The normalized spherical harmonics are defined as \begin{equation} Y_n^m(\theta, \phi) =\sqrt{\frac{(2n+1)}{4\pi}\frac{(n-m)!}{(n+m)!}}P_n^m(\cos\theta)e^{im\phi}, \quad n = 0, 1, 2, \cdots, \quad |m| < n \end{equation} The index n is the degree of the spherical harmonic and refers to the polynomial degree of the function. The index m is the order; it ranges from -n to n. As a result, for degree n spherical harmonics, there are 2n + 1 orders. The order m for fixed degree n are closely related to rotations on the sphere.
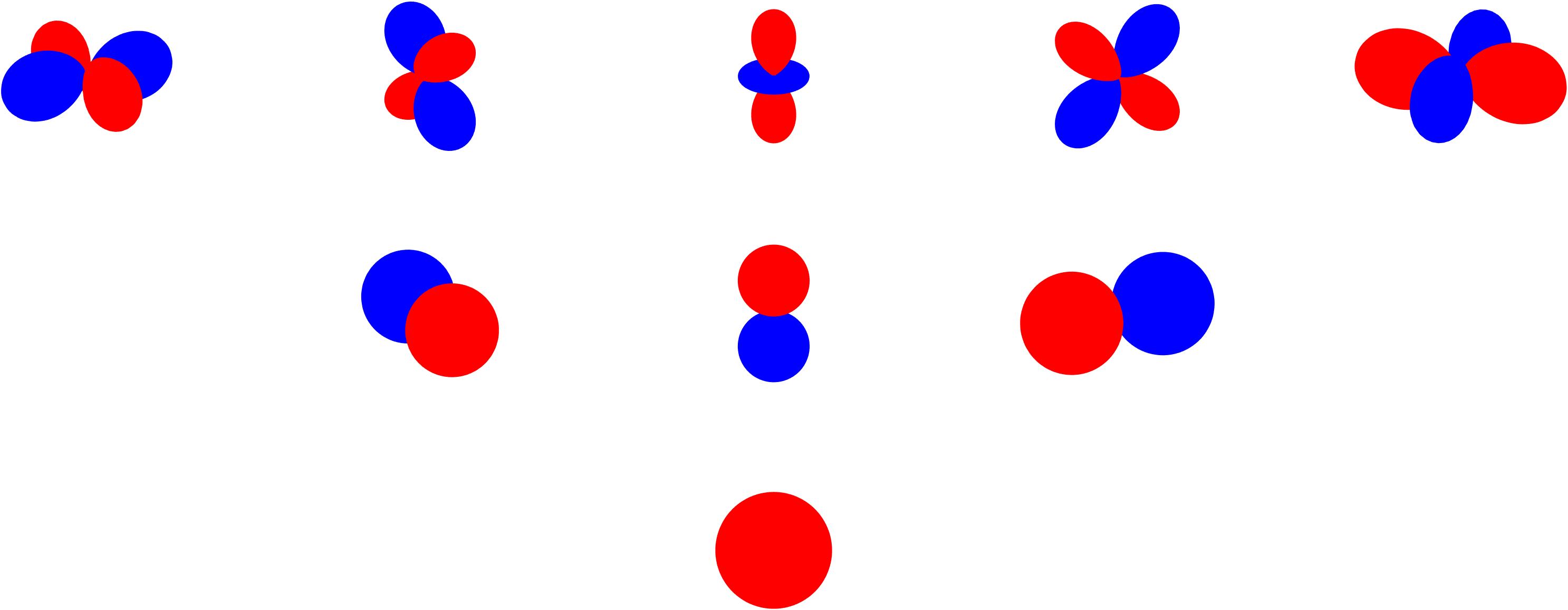
These spherical eigenfunctions form an orthonormal basis on the sphere so that a function may be expanded in a generalized Fourier series as \begin{equation} f(\theta,\phi) = \sum_{n=0}^\infty \sum_{m=-n}^n f_n^m Y_n^m(\theta,\phi) \end{equation} where \(f_n^m\) are the expansion coefficients. The expansion coefficients follow by applying ‘Fourier’s trick.’ First, multiply each side of the expansion by a conjugated spherical harmonic of arbitrary degree p and order q \begin{equation} f(\theta,\phi)\left[Y_p^q(\theta,\phi)\right]^* = \sum_{n=0}^\infty \sum_{n=-m}^m f_n^m Y_n^m(\theta,\phi)\left[Y_p^q(\theta,\phi)\right]^* \end{equation} integrating over the sphere \begin{equation} \int_0^\pi \int_0^{2\pi}f(\theta,\phi)\left[Y_p^q(\theta,\phi)\right]^* \sin\theta d\theta d\phi= \sum_{n=0}^\infty \sum_{m=-n}^n f_n^m \int_0^\pi \int_0^{2\pi} Y_n^m(\theta,\phi)\left[Y_p^q(\theta,\phi)\right]^*\sin\theta d\theta d\phi \end{equation}
applying orthogonality gives\begin{equation} \int_0^\pi \int_0^{2\pi}f(\theta,\phi)\left[Y_p^q(\theta,\phi)\right]^* \sin\theta d\theta d\phi= \sum_{n=0}^\infty \sum_{n=-m}^m f_n^m\delta_{np}\delta_{mq} \end{equation} so that \begin{equation} f_n^m = \int_0^\pi \int_0^{2\pi}f(\theta,\phi)\left[Y_n^m(\theta,\phi)\right]^* \sin\theta d\theta d\phi. \end{equation}