optimization methods
Optimization algorithms try to minimize a function.
In gradient descent, the iterative update is related to the local gradient of the objective function \begin{equation} \mathbf{x}^{(k+1)} = \mathbf{x}^{(k)} - \mu \nabla J(\mathbf{x}^{(k)}). \end{equation}
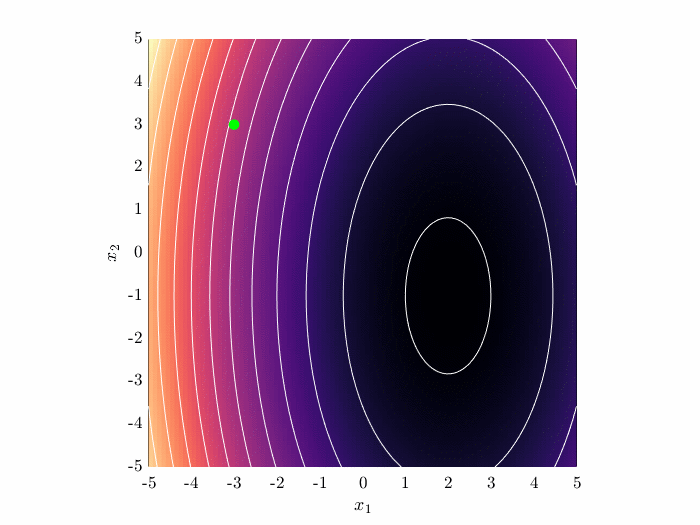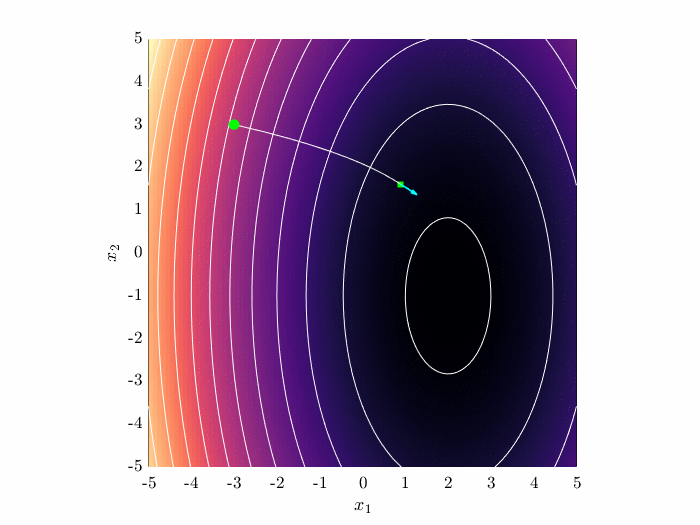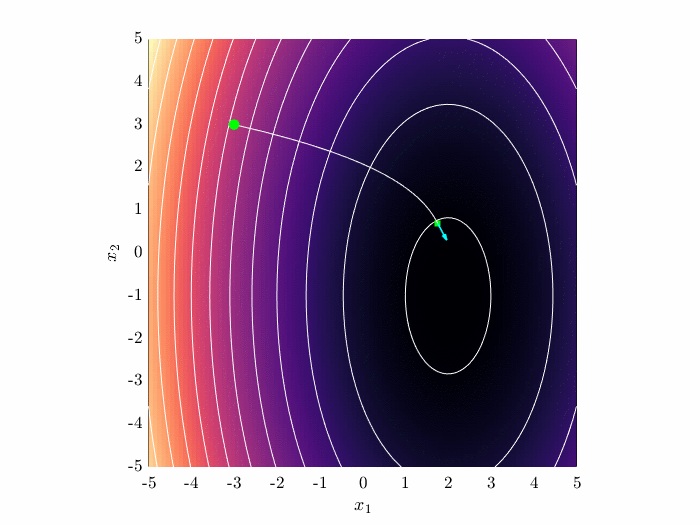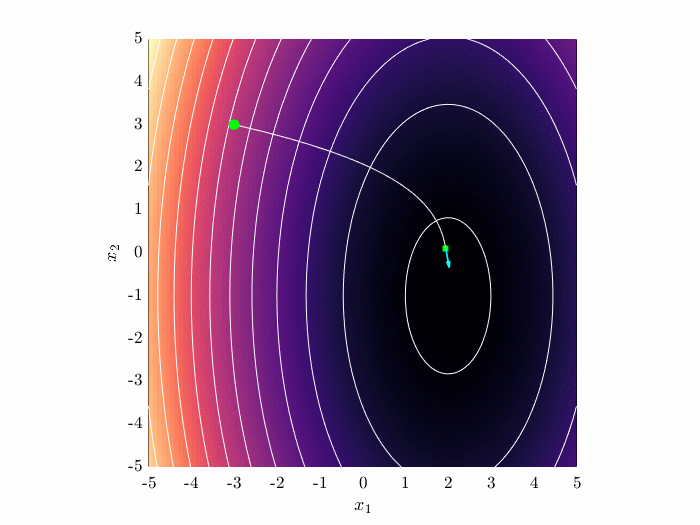
Gradient descent algorithm
Newton’s method uses the Hessian matrix to compute the local curvature. This leads to a more direct descent path. However, computing the Hessian matrix may be difficult for some problems.
\begin{equation} \mathbf{x}^{(k+1)} = \mathbf{x}^{(k)} - \mathbf{H}^{-1}(\mathbf{x}^{(k)})\nabla J(\mathbf{x}^{(k)}). \end{equation}
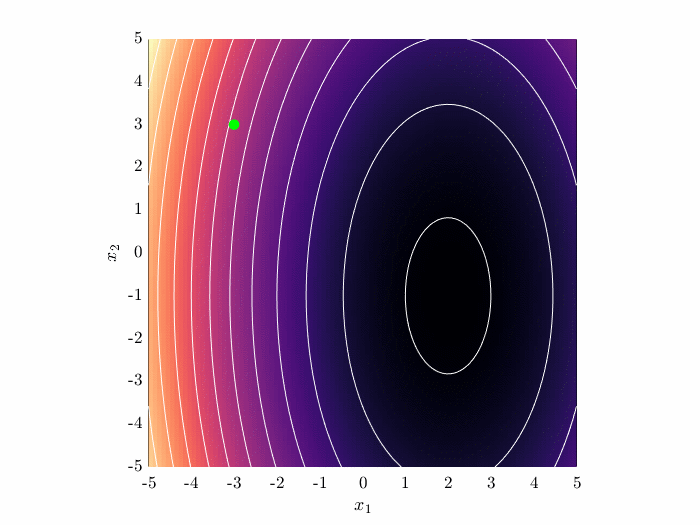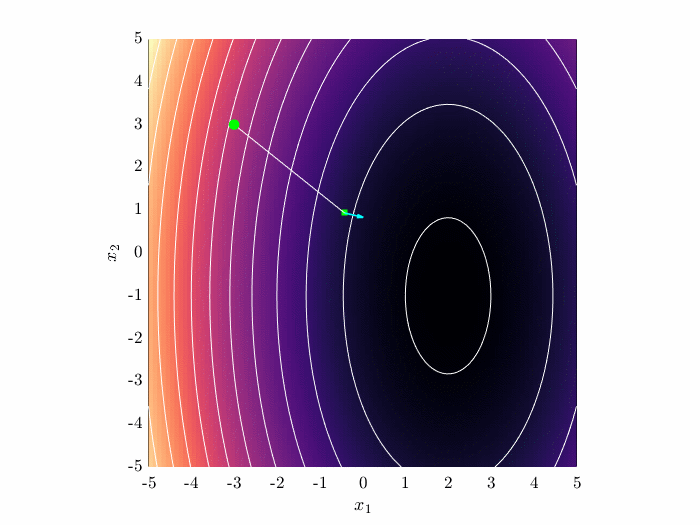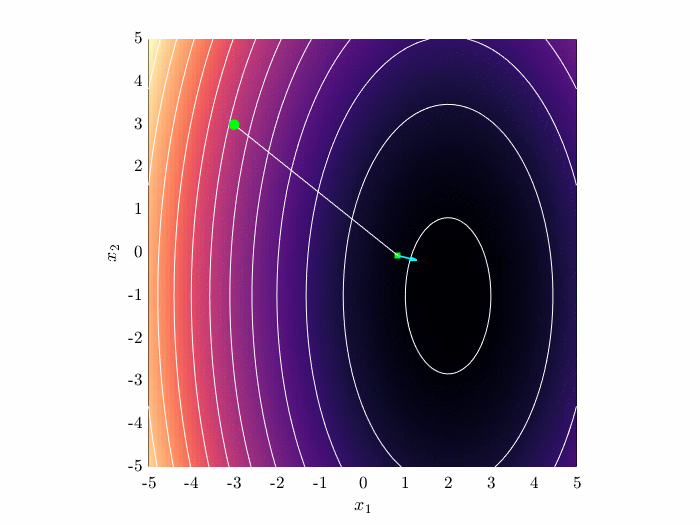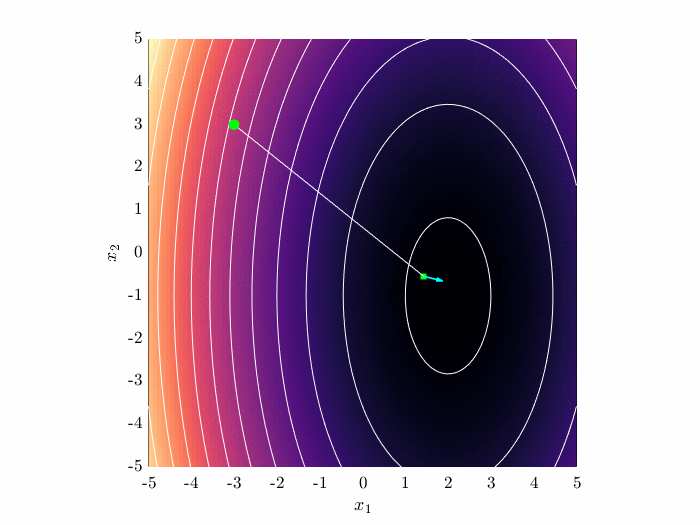
Newton's method