convolution operation
The output \(y(t)\) of a linear, time-invariant system is given by the convolution of its impulse response \(h(t)\) with the input \(x(t)\) \begin{equation} y(t) = \int_{-\infty}^\infty x(\tau) h(t - \tau)d\tau. \end{equation} For discrete-time systems, the convolution sum is \begin{equation} y[n] = \sum_{m=-\infty}^\infty x[m]h[n-m] \end{equation} The sum can be interpreted as the superposition of delayed and scaled impulse responses:
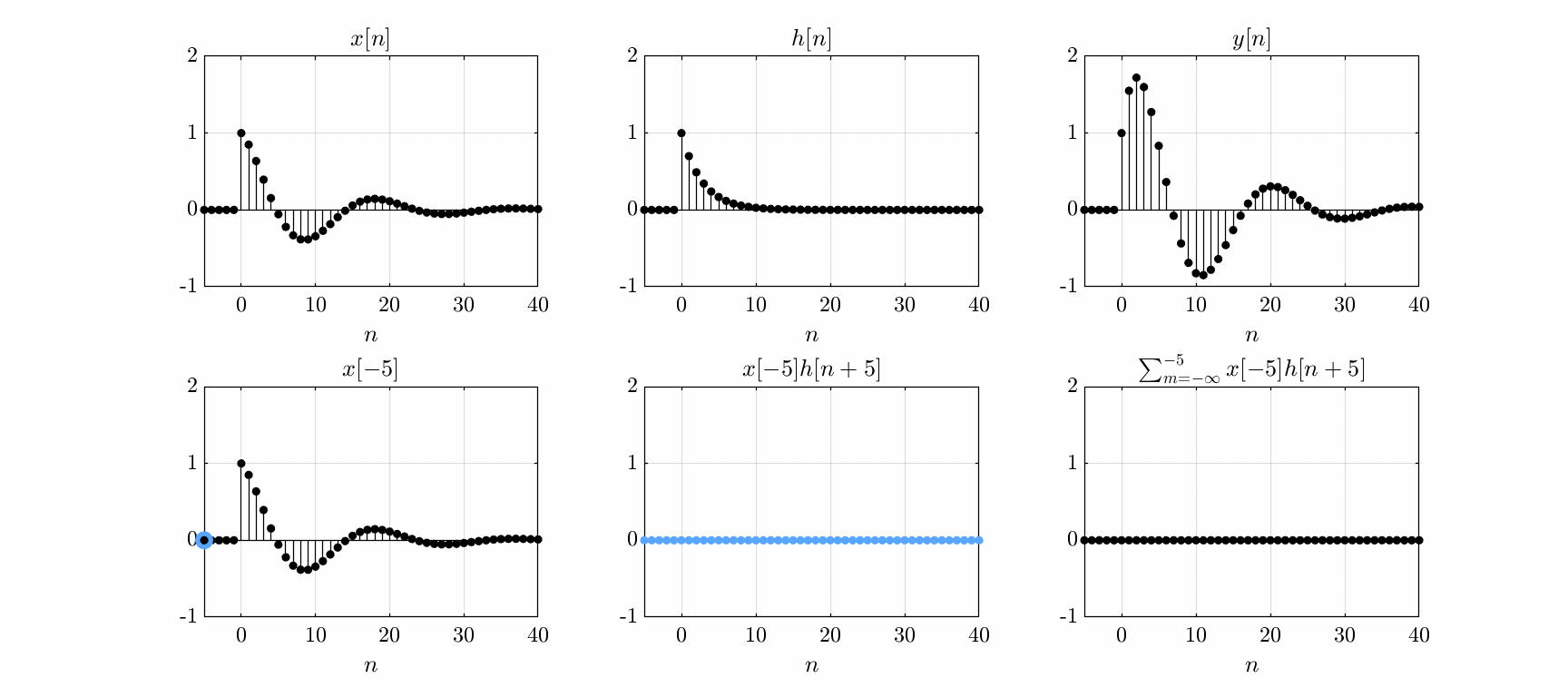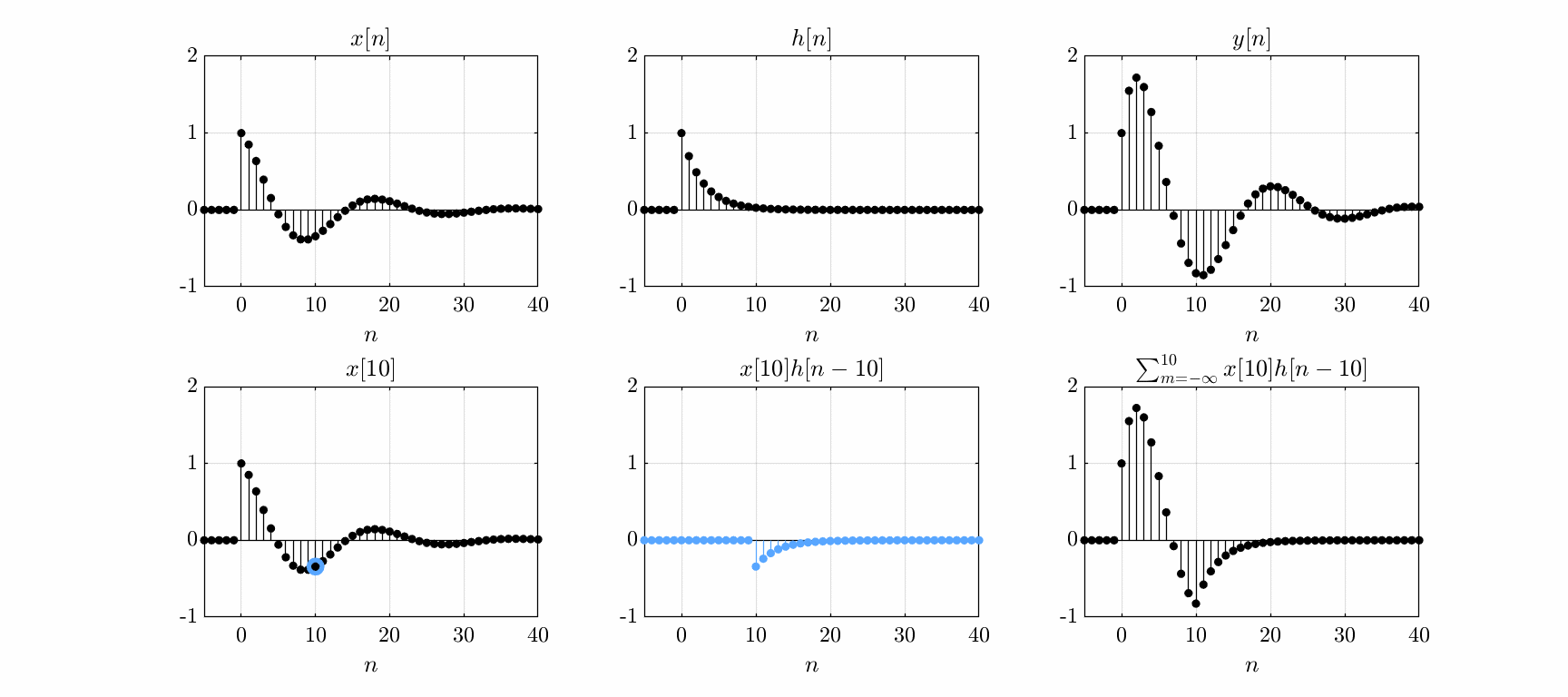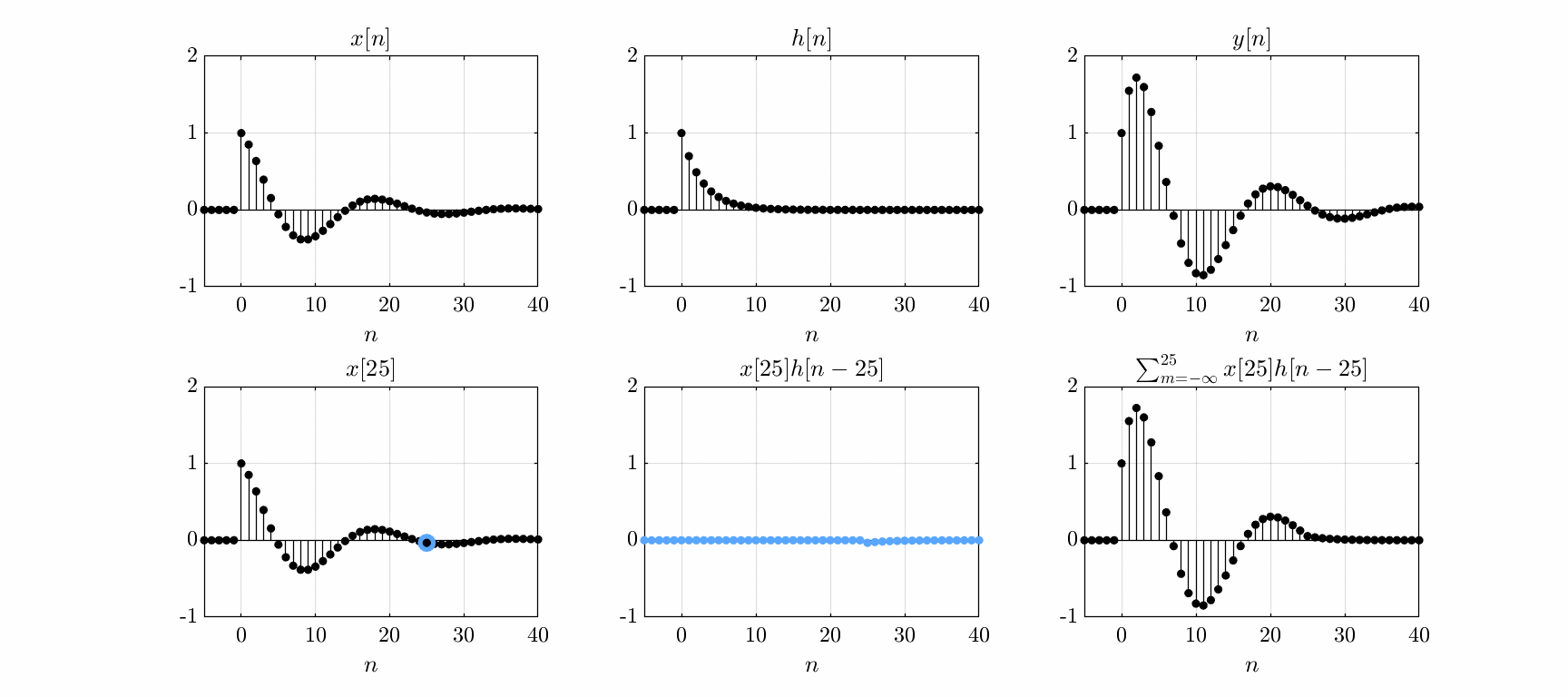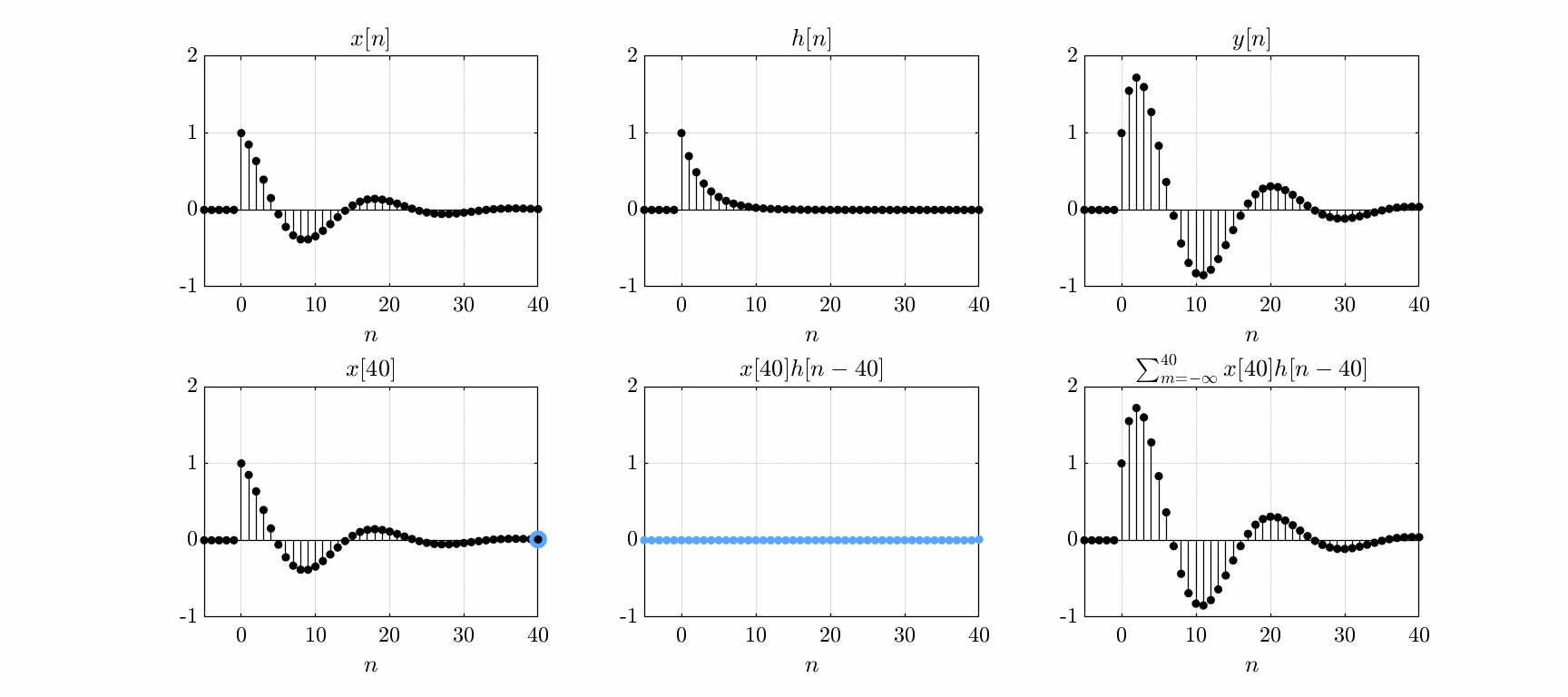
Convolution of an input signal with a system impulse response.
Another common interpretation of convolution is the graphical approach, where the output is the area under the curve of the product of the input and the time-reversed impulse response:
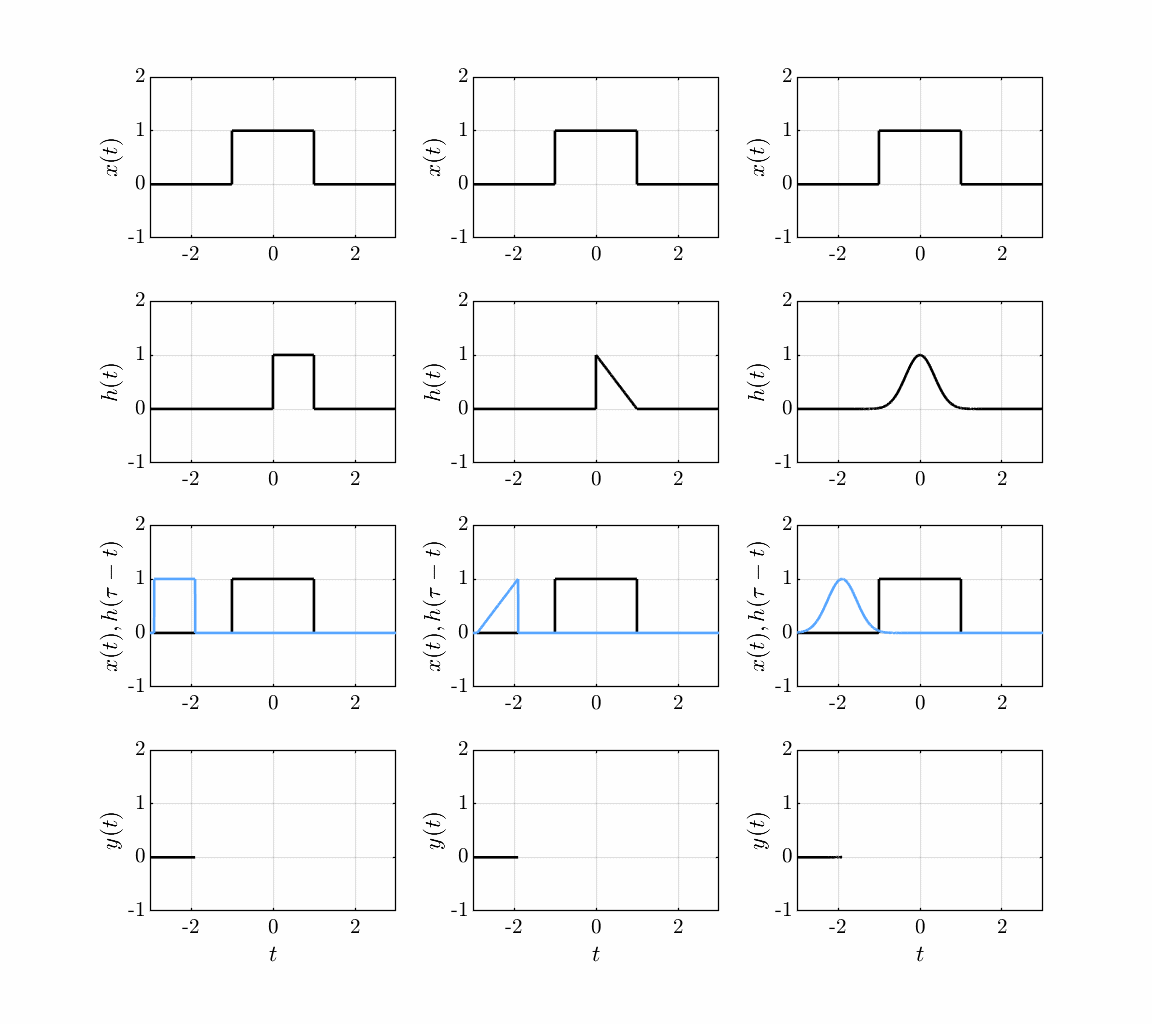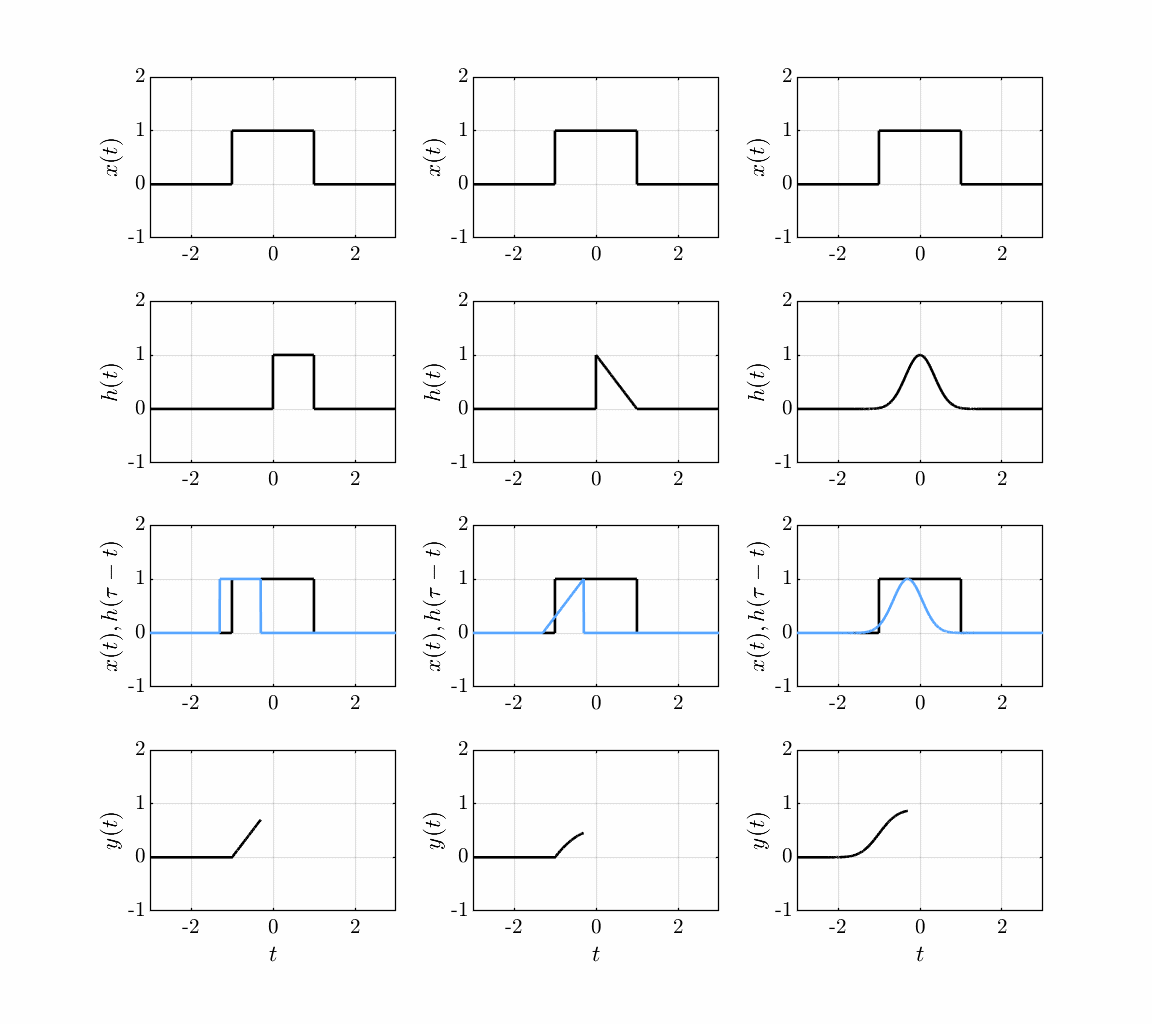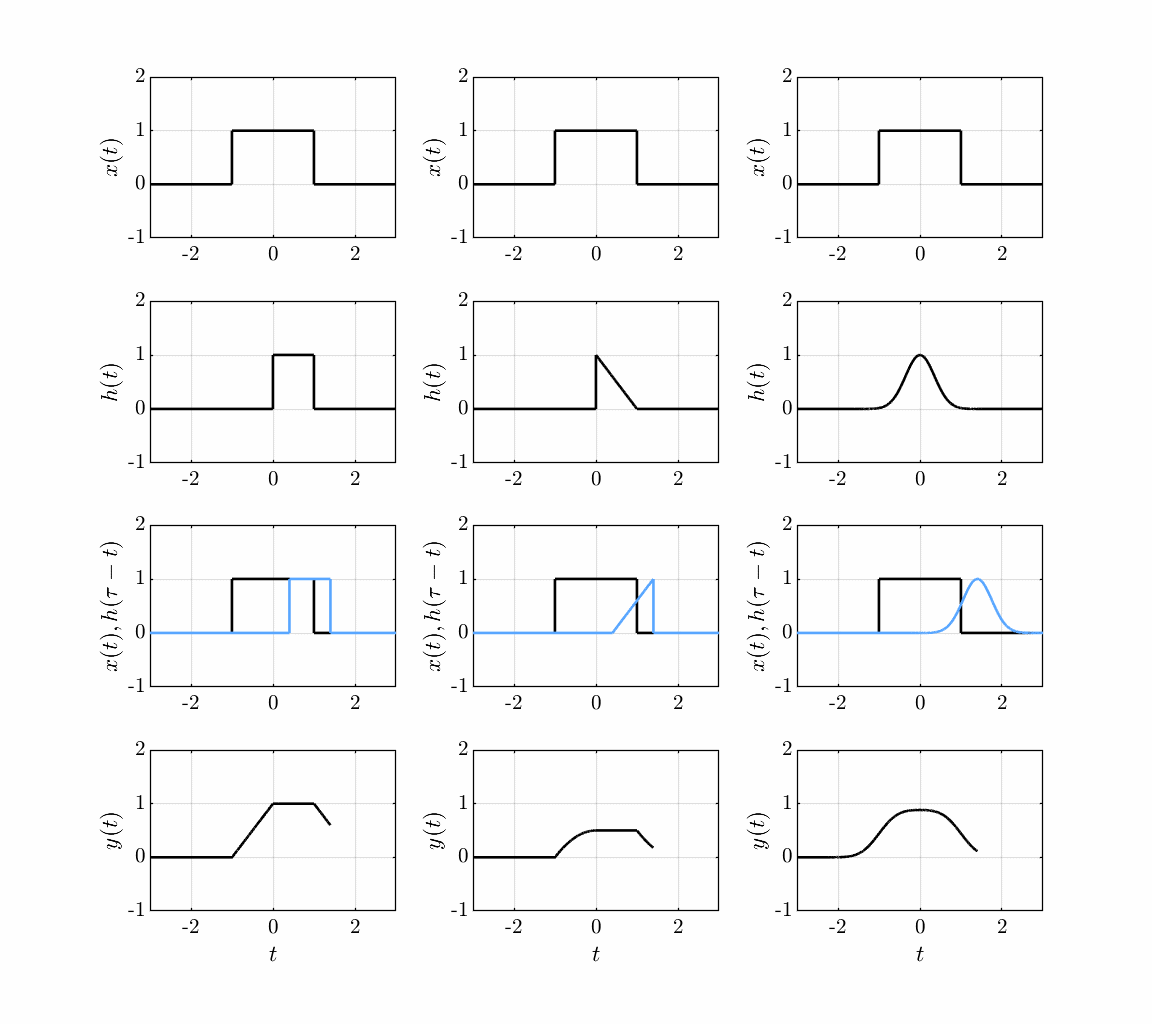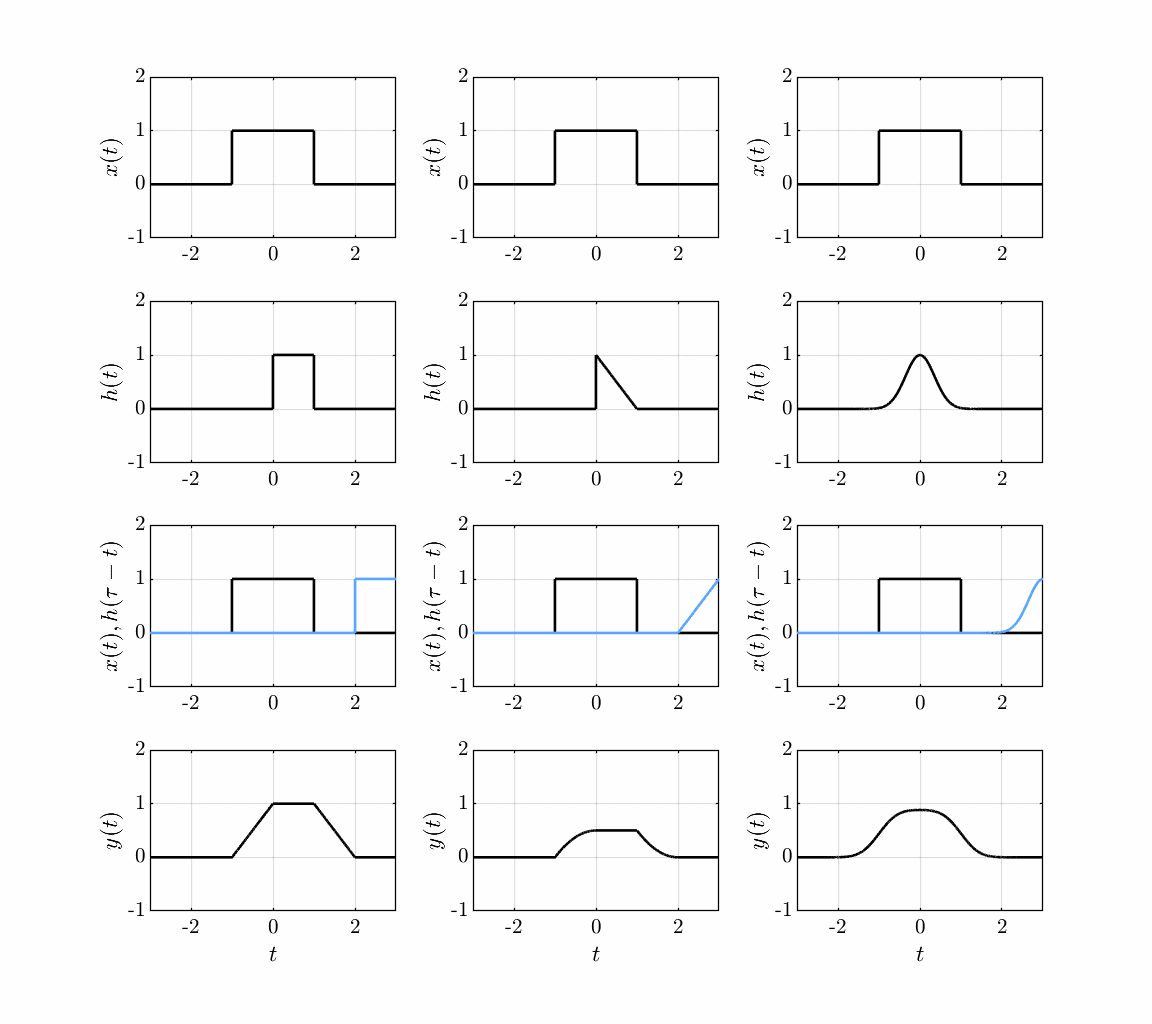
Convolution of an input signal with a system impulse response.